Durante este
siglo, el mundo va a sufrir una crisis en la que colaboraran, influyéndose
mutuamente, factores culturales, biológicos, económicos y políticos.
El aspecto más
positivo de este siglo reside en su aportación científica, aunque
no existe especialización. De ahí que una misma persona pueda cultivar
diversas ramas del saber.
El conocimiento
es racional y desde el punto de vista metódico. Los métodos discursivos
y librescos fueron sustituidos por la observación y la experimentación.
En efecto, la ciencia se revolucionó con las ideas del inglés Francis
Bacon (1581-1627) sobre la adecuada organización de las ciencias.
La Química,
como ciencia racional, comienza a desprenderse de la alquimia. La
generalización de la disección de cadáveres y el descubrimiento
del microscopio harán conocer mejor el cuerpo humano.
La filosofía
se hará en el estricto racionalismo y prescindirá no sólo de las
creencias escolásticas, sino también de las opiniones de los antiguos
filósofos. Es, pues, una rotura con el sistema escolástico basado
en Aristóteles y la Revelación.
El Barroco matemático
Se denominara
así al periodo que va desde la muerte de Viète, acaecida en 1603,
hasta la fecha del nacimiento del matemático suizo Leonhard Euler,
en 1707.
Durante este
periodo se va a crear la Geometría analítica; los números indo-arabigos
desplazaran definitivamente a los números romanos; progresará la
notación y se inventarán los logaritmos y el cálculo infinitesimal.
Todos estos
progresos harán posibles los de la física.
Progresos científicos
Las ideas que
detallo el inglés Bacon sobre la adecuada organización de las ciencias
van a ser utilizadas durante este siglo. Estas ideas consistían
básicamente en los pasos siguientes:
- Había que reunir tantos hechos o datos como fuera
posible
- Disponerlos en orden lógico para formar una hipótesis
o teoría
- La teoría o hipótesis debe comprobarse mediante la
experimentación
En medicina
se popularizó la obra "Sobre la estructura del cuerpo humano"
del belga André Vésale (1514-1564), en la cual expone, basándose
en la disección de cadáveres, unos estudios sobre el cuerpo humano
que darían origen a lo que hoy llamamos anatomía.
Las investigaciones
de Malpighi (1628-1694) y de W. Harvey (1578-1675) les conducen,
respectivamente al descubrimiento de los capilares en los animales
y en el hombre, y cómo circula la sangre por las arterias y venas
en el hombre.
El padre de
la citología, esto es el estudio de las células, fue le ingles Robert
Hooke (1635-1703), el cual comprobó que las plantas se componían
de diminutas unidades. A partir de este descubrimiento se originaría
en el siglo XIX la teoría celular.
El holandés
A. Leeuwenhoek (1632-1723) encontró las bacterias e investigó la
estructura de los vegetales y de los animales.
En 1680, el
inglés Isaac Newton enuncia la Ley de Gravitación Universal.
El italiano
Galileo Galilei, quien inventó el termómetro y desarrolló el telescopio
y el microscopio propone su teoría sobre la caída de los graves.
El francés Blaise
Pascal, escribió dos tratados, uno sobre el equilibrio de los líquidos
en el cual expone el principio que lleva su nombre y que dice: Toda
presión ejercida sobre un líquido es transmitida íntegramente a
todos los puntos de su masa y actúa perpendicularmente sobre las
paredes que lo contienen; y el otro sobre el peso de la masa
de aire.
El inglés Robert
Boyle, quien, además de iniciar en química el empleo del tornasol,
perfeccionó la máquina neumática y formuló la ley que lleva su nombre
unido al del francés Mariotte, y que dice: La presión de una
masa fija de un gas por el volumen que ocupa es una constante para
cada valor de la temperatura.
El alemán Otto
von Guericke inventó la máquina neumática, una balanza para pesar
el aire, un barómetro, una máquina electrostática y realizó el célebre
experimento de acoplar por los bordes dos hemisferios huecos de
cobre e hizo el vacío en la esfera resultante intentando separarlos
por tracción, lo que no consiguió pese a haber enganchado varios
caballos a cada uno. Sin embargo, al abrir la llave para que entrase
el aire se separaron ambas piezas sin el menor esfuerzo.
El italiano
Evangelista Torricelli (1608-1647) expuso la regla que lleva su
nombre para calcular la velocidad de salida de un líquido por el
orificio de un vaso; inventó el barómetro de cubeta, creando por
primera vez un vacío absoluto en el tubo barométrico.
Mecánicas para acelerar el trabajo
de cálculo
Uno de los medios
de que se valió el hombre para hacer sus cálculos fue el ábaco.
Desde los tiempos más antiguos esta invención se transmitió de civilización
en civilización. Todavía hoy, el ábaco es un computador muy corriente
en algunos pueblos de Asia, en donde no es muy difícil encontrar
personas que calculan más de prisa que los oficinistas con las máquinas
calculadoras.
Durante el siglo
XVII fue muy popular el invento del escocés John Neper (1550-1617)
para multiplicar, conocido como rodillos de Neper. Pero mucho más
importante para la matemática fue lo que hoy conocemos con el nombre
de Logaritmos. Un logaritmo es el exponente a que hay que elevar
un número para obtener otro número. Al familiarizarse con ellos
se abrevian considerablemente los cálculos de productos, cociente,
potencias, raíces y operaciones combinadas de las anteriores. Esta
fue la intención de Neper, el mismo que empleó por primera vez la
coma decimal.
Antes de publicar
sus resultados, es posible que reflexionara sobre las sucesiones
de las potencias de un número. En estas es evidente que los productos
o cocientes de las potencias corresponden, respectivamente, a las
sumas o diferencias de los exponentes de las mismas potencias.
Al parecer,
lo que animó a este escocés a publicar en 1614 su obra Descripción
de la maravillosa regla de los Logaritmos fue el tener noticia
del método de la prostafaireses, muy utilizado en los cálculos astronómicos.
En esencia,
Neper, mostró que todo número puede expresarse en términos del número
10, elevado a tal o cual potencia. Es decir, de la misma manera
que 1000 = 103, 2 es 100.3010300.
Debido a su avanzada edad, no pudo llevar
a la práctica sus ideas, que fueron recogidas por Henry Briggs (1561-1639),
quien comenzó a partir de la igualdad log 10 = 1 y después fue calculando
otros logaritmos tomando raíces sucesivas: Por ejemplo, de 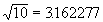 ,
obtiene Briggs que log 3.162277 es 0,5. ,
obtiene Briggs que log 3.162277 es 0,5.
Calculando de
esta manera halló otros logaritmos decimales de los números del
1 al 1000, con catorce cifras decimales, que además de gozar de
las propiedades generales de los logaritmos, cumplen que solamente
las potencias enteras de 10 tienen logaritmo entero; los restantes
números tienen un logaritmo compuesto de una parte entera, llamada
característica, y otra decimal, llamada mantisa.
Mientras Briggs
se ocupaba de dichas tablas, John Speidell calculaba los logaritmos
naturales o neperianos de las funciones trigonométricas. Este sistema
de logaritmos, que tienen por base el numero "e", aparecen
publicados en la obra de Speidell titulada Nuevos Logaritmos
y que fue publicada en 1619. No obstante, anteriormente ya habían
aparecido algunos logaritmos naturales en la traducción de la obra
de Neper, hecha por E. Wright en 1616.
Conviene poner
en manifiesto que si bien es cierto que John Neper fue el primero
en publicar la idea de logaritmo, también lo es que el mismo tiempo
en esa idea trabajaba en forma independiente el suizo Jobst Bürgi.
Otra de las
maravillas mecánicas para acelerar el trabajo del cálculo durante
este siglo es la fantástica máquina inventada por Blaise Pascal,
quien además hizo algunos aportes importantes a la matemática.
El progreso Notacional
El simbolismo
matemático ha ido evolucionando a lo largo del tiempo.
La operación
de dar el oportuno símbolo a un ente, o una relación o combinación
entre ellos se lama Notación.
Durante este
siglo XVII, fue introducido el signo de x para la multiplicación
por el clérigo inglés William Ouglthed (1574 - 1660) y el flamenco
Simon Stevion (1548 - 1620), el mismo que popularizó la utilización
de las fracciones decimales mediante su obra Décimo o De
Thiende, impresa en 1585, formuló el convenio de que 1/3 dentro
de un círculo significaría una raíz cúbica y que 3/5 en un círculo
representaría la raíz quinta del cubo.
Descartes popularizó
el símbolo = de Recorde y utilizó x2 en vez de xx.
John Wallis
utilizó el signo 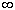 para designar el infinito. para designar el infinito.
No obstante,
el mayor creador de notación es Leibniz, quien propuso el símbolo
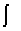 para la integral. Que es una s alargada inicial de la palabra
suma, dx y dy para diferenciales o diferencias más pequeñas posibles.
Además es el primer matemático relevante que emplea el signo · y
: para multiplicar y dividir; el signo ~ para designar "semejante
a" y para la integral. Que es una s alargada inicial de la palabra
suma, dx y dy para diferenciales o diferencias más pequeñas posibles.
Además es el primer matemático relevante que emplea el signo · y
: para multiplicar y dividir; el signo ~ para designar "semejante
a" y 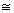 para "es
congruente con" para "es
congruente con"
Un gran pensador: René Descartes
(1596 - 1650)
La gran influencia
de los jesuitas en el barroco fue muy grande y se manifestó igualmente
en el terreno del pensamiento y la educación que en el del arte
y la literatura.
En la enseñanza,
los jesuitas no querían formar monjes alejados del mundo, sino laicos
que sirvieran fielmente a la Iglesia, lo cual motivó su empeño en
instruir el las ciencias profanas, adaptándose de esta forma al
espíritu de la época. En sus cuadros de enseñanza figuraban el estudio
fundamental de los idiomas y de los escritores de la antigüedad,
las Matemáticas, la Teología y la Filosofía. Toda esta serie de
conocimientos, se armonizaba en los discípulos de los jesuitas.
En el colegio
de jesuitas de La Flèche, se educó el francés René Descartes, quien
en 1616 se licencia en derecho por la Universidad de Poitiers.
No satisfecho
con los conocimientos adquiridos e independiente en su posición
económica, Descartes cerró los libros para dedicarse el estudio
del mundo. Después de probar brevemente la vida en sociedad, concretamente
la parisina, se convierte en soldado en 1617.
Mientras fue
soldado se convenció de que el mundo necesitaba una fórmula que
disciplinara el pensamiento racional y unificara el conocimiento.
En ninguna parte encontraba descartes la seguridad y certeza de
los resultados que perseguía, sólo las matemáticas colmaban semejante
aspiración. Por eso, él mismo dice: "Cuando era soldado, pasaba
la mayor parte del tiempo con la cabeza y las orejas en el estudio
de las matemáticas."
Esta rama del
conocimiento le gustaba, debido a la certidumbre de sus pruebas
y a la evidencia de sus razonamientos.
Esta visión
de Descartes originó la doctrina de que todo conocimiento, tanto
pasado como futuro debía elaborarse en términos de razonamiento
matemático. De este modo es como descartes propone a los intelectuales
contemporáneos que dejaran de fiarse tan ciegamente de las ideas
antiguas y empezaran de nuevo a tratar de explicar la Naturaleza
a través de un esquema científico deductivo.
Esta filosofía
la explicitó en una publicación que después la suprimió como deferencia
a su fe católica, ya que suscribía con ellas las ideas de Copérnico
en torno al Universo.
A causa de que
París no le ofrecía el reposo necesario para recoger sus pensamientos,
en 1629 se retira a Holanda. Allí vivirá veinte años. En 1637, publicó
su Discurso del Método para dirigir correctamente la razón,
conocida también como el Método. Esta obra, que será fundamental
en la filosofía, lo situará como uno de los grandes pensadores del
Barroco. No obstante, su filosofía despertó, en los partidarios
de la doctrina medieval un odio que se transformó muy pronto en
prohibiciones y persecuciones personales. Debido a ello y a una
invitación de la Reina Cristina de Suecia, abandonó su residencia
de los países bajos y se trasladó a Estocolmo en 1649.
Debido a la
crudeza del clima y a su débil salud, enfermó y falleció en 1650
en esa misma cuidad.
Las reglas cartesianas para
una buen método
Los filósofos
griegos se habían preguntado por la posibilidad y naturaleza de
nuestro conocimiento, pero predominantemente estas cuestiones tenían
para ellos, así como para los filósofos medievales, un matiz ontológico:
al preocuparse del problema de conocer, cuyos polos son el sujeto
que conoce y el objeto conocido, se fijan más en el segundo que
en el primero.
La filosofía
moderna se centra en el sujeto cognoscente. Aunque el interés por
este problema comienza con Descartes, Leibniz, Loake, Berkeley,
Hume y algún otro, solo tomará casi exclusivismo con Immanuel Kant,
como veremos más adelante.
Descartes quiere
construir una ciencia sobre las cosas que sean absolutamente ciertas,
una filosofía en la que no quepa ninguna duda, para ello debe utilizar
un método (del griego: camino). Nosotros la podemos definir, aquí,
como el camino que conduce nuestra inteligencia a la verdad.
Descartes da
cuatro reglas para un buen método :
- Partir de principios claros y evidentes.
- Dividir cada una de las dificultades que se examinan,
en cuantas partes sea posible.
- Conducir ordenadamente los pensamientos, empezando
por los objetos más simples para ascender hasta el conocimiento
de los más compuestos.
- Hacer revisiones generales para estar seguro de no
omitir nada.
La Géométrie
Descartes concluyo
su obra con tres ejemplos concretos sobre como podía ser aplicado.
Los dos primeros pretendían explicar el comportamiento de las lentes
y el movimiento de los astros. El tercero, un extenso apéndice de
106 páginas fue La Géométrie.
Aunque La
Géométrie es un tratado teórico sin ninguna intención práctica,
jugará un papel trascendente en el futuro de las matemáticas. Su
influencia originará la geometría analítica, cuyos problemas fundamentales
son:
- Dada una ecuación, hallar el lugar geométrico que
representa.
- Dado un lugar geométrico definido por determinadas
condiciones, hallar su ecuación matemática.
En esencia,
la geometría analítica consiste en la aplicación del álgebra al
análisis geométrico mediante el establecimiento de ciertos convenios,
fundamentalmente la creación de un sistema de coordenadas que permite
individualizar cada punto por un par de números para la geometría
analítica plana y por tres números para la geometría analítica del
espacio.
A partir del
concepto de coordenadas, esta nueva rama matemática dará a los matemáticos
un nuevo enfoque para el tratamiento de la información matemática.
La geometría
analítica transformará todo el conocimiento antiguo de forma tal
que ramas del conocimiento matemático que parecías diferentes, como
la trigonometría y los logaritmos, las absorbió y les dio un alcance
más completo. Gracias a su desarrollo derivara un concepto fundamental
para las matemáticas, como es la idea de funciones y variables,
las cuales tendrán, también, una gran utilidad para la experimentación.
El científico experimental puede transformar los resultados de una
experiencia en una ecuación y después representarla o viceversa.
Si después al repetir la anterior experiencia con mucho cuidado
para que las condiciones no varíen, obtiene la misma ecuación, puede
llegar a formular una ley que puede interpretarse por medio de palabras
e ideas. Una vez enunciada dicha ley, puede combinarla con otras
fórmulas para sugerir nuevas posibilidades.
Además , la
geometría analítica, al permitir una gran amplitud de puntos de
vista, no sólo dará buenos resultados en otras ramas matemáticas,
como por ejemplo la geometría proyectiva, sino que será responsable
en buena parte del origen de la rama matemática que conocemos hoy
con el nombre de análisis, la cual abarca gran parte de las matemáticas
inventadas desde la época de Descartes, y que en su aceptación más
general comprende la aritmética. El álgebra, el cálculo infinitesimal
(diferencial e integral), la teoría de funciones reales y complejas,
así como la teoría de las ecuaciones diferenciales.
Por ultimo,
se debe poner en manifiesto que la Géométrie tenía dos inconvenientes,
a saber: Había sido publicada en francés y, además era una obra
de difícil comprensión para la mayoría de los contemporáneos de
Descartes, debido a que éste omitió en ella muchos detalles elementales.
Evolución de la Geometría Analítica
Los inconvenientes
señalados fueron superados cuando el profesor de matemáticas holandés
Frans van Schooten (1615 - 1660) hizo imprimir, en 1649 una versión
en latín de La Géométrie, ampliada con unas aclaraciones
tales como las demostraciones realizadas por Debeaune de que las
ecuaciones y2 = xy + bx; y2 = 2dy + bx; y2
= bx - x2, representan, respectivamente, hipérbolas,
parábolas y elipses.
Esta obra titulada
Geometría por René Descartes volvió a aparecer en 1659 en
una segunda edición nuevamente ampliada con la obra de Jan Witt
(1629 - 1673) titulada Elementa curvarum, en la que reduce
todas las ecuaciones de segundo grado e x e y a formas canónicas.
Pero sin lugar
a dudas, uno de los que más contribuyeron en la evolución de la
geometría analítica fue el mejor discípulo de Schooten, es decir,
Christian Huygens (1629 - 1659), el cual al hallar los puntos máximos
y mínimos y el punto de inflexión logro ser uno de los primeros
en dibujar una curva correctamente.
El interés de
Huygens por los relojes de péndulo le condujo a hacer investigaciones
sobre la involutas y evolutas. Las cuales aparecen expuestas junto
a importantes resultados de mecánica en su obra Horolagium Oscillatorium,
publicada en 1673 y que tendrá una cierta influencia en la obra
Los Principia de Newton.
Otra contribucion
muy importante fue la del francés Pierre Fermat (1601 - 1665) con
su obra titulada Introducción al los lugares geométricos planos
y sólidos, que no fue publicada en vida de su autor, pero que
circuló en forma manuscrita.
En ella, emplea
Fermat una geometría analítica más próxima a la que utilizamos en
la actualidad que a la de Descartes. No obstante, al igual que Descartes,
no utiliza abcisas negativas e intuye la posibilidad de una geometría
analítica de más de dos dimensiones.
Si a Schooten
se le suele considerar como el impulsor de la geometría analítica
en el continente europeo, el Inglaterra lo fue el catedrático de
Geometría de Oxford John Wallis (1616 - !703), quien en 1655 publicó
Tractary de Sectionibus Conics, en la que da la definiciones
de la elipse y de la parábola como lugar geométrico de los puntos
cuyas coordenadas satisfacen la ecuación de segundo grado con dos
variables y además reemplaza sistemáticamente los conceptos geométricos
por los aritméticos.
En 1691, en
la revista Acta eruditorum aparece un trabajo del suizo Jacques
Bernoulli (1654 - 1705), en el que utiliza las coordenadas rectangulares
y polares.
La geometría proyectiva
La parte de
la geometría que estudia las propiedades que se conservan en una
proyección se denomina geometría proyectiva. El iniciados de esta
rama fue el francés Girad Desargues (1591 - 1661), quien en 1639
publica su obra Borrador de un ensayo que trata de los encuentros
de un cono con un plano. En esta obra Desargues aceptó la idea
de Kepler de que la parábola tiene un foco en el infinito y que
dos rectas se cortan en el infinito. Un cilindro, por ejemplo, es
para Desargues un cono cuyo vértice está en el infinito.
Partiendo de
las ideas de la perspectiva del arte renacentista de que las formas
y los tamaños aparentes cambian según cambia el plano de incidencia
que corta al cono de los rayos visuales, Desargues observó la existencia
de propiedades que permanecen invariables bajo tales cambios y estas
son las que estudiará la geometría proyectiva. Es decir, si desde
un punto exterior trazamos rectas que unan este punto a una recta,
curva, plano o superficie y cortamos estas rectas por una plano,
la geometría proyectiva estudiará las propiedades de los puntos
de corte.
Este tipo de
geometría que no se interesa por las distancias entre puntos ni
por los ángulos entre rectas o planos, sino por las posiciones relativas
de estos elementos en el espacio, no fue aceptada por los matemáticos
de la época, al considerarla sin sentido.
Por los tanto,
las ideas de Desargues no recibieron una buena acogida y quizá influyo
mucho en ello que su alumno con más porvenir en la matemática, Blaise
Pascal, abandonó a finales de 1654 las matemáticas por la teología,
y sólo volverá a los estudios matemáticos durante un periodo muy
breve, entre 1658 y 1659.
Blaise Pascal (1623 - 1662)
Pascal fue una
matemático francés muy precoz, ya que a los 16 años había publicado
la obra titulada Ensayo de Cónicas, en donde cita a Desargues como
fuente de inspiración. A la edad de 18 años cambió de actividad
y diseñó su maquina calculadora.
En 1648 trabajó
en la hidrostática, posteriormente volvió a escribir una obra completa
sobre las cónicas, pero no llego a publicarla.
Además de estas
contribuciones, participó en la fundamentación de las bases del
cálculo de probabilidades, a tratar posteriormente.
Los infinitesimales
A finales del
siglo XVI y sobre todo durante el siglo XVII, los matemáticos para
resolver problemas prácticos recurren aisladamente al razonamiento
sobre lo infinitamente pequeño y lo infinitamente grande, pero raras
veces a través de las rigurosas pruebas griegas. Así, por ejemplo,
el ya citado Stevin, en su obra Estática, publicada en 1586, demuestra
donde está situado el centro de gravedad de un triángulo mediante
su división en un conjunto de fajas infinitamente estrechas.
También Fermat,
en su obra Metodo para hallar máximos y mínimos, expone un procedimiento
que consiste en cambiar ligeramente el valor de las variables para
considerar valores próximos a uno dado. A pesar de que Fermat no
disponía del concepto de límite, utiliza un camino muy similar al
que utilizamos actualmente para este tipo de problemas. Además,
Fermat, también utilizó los infinitesimales para calcular el área
bajo una curva por medio de la división de la misma en rectángulos.
El alemán Johan
Kepler (1571 -1630) utiliza los infinitesimales no únicamente para
calcular el volumen de las cubas de los vinateros, sino también
para resolver problemas relativos a áreas.
Para el italiano
Galileo Galilei (1554 - 1642) lo infinitamente pequeño tenía gran
importancia, pues lo necesitaba para su dinámica, en sus obras ya
sugería el principio general: una ecuación en la que intervienen
infinitésimos de orden superior pueden despreciarse por que no afectan
al resultado final. Su intención de escribir una obra sobre le infinito
en Matemática no lo llevo a cabo él sino su discípulo Bonaventura
Cavalieri (1598 - 1647), quien publica en 1635 su obra Geometría
Indivisibilis Continuorum, en que la idea fundamental es la
de considerar el área formada por segmentos rectilineos o indivisibles
y un volumen sólido como un compuesto de secciones indivisibles.
Esta obra de Cavalieri va a facilitar enormemente el problema de
las cuadraturas de las curvas - cálculo de la superficie comprendida
entre el eje de abcisas un arco de curva u loas dos ordenadas que
lo limitan - ya que en ella expone el teorema geométrico que viene
a ser el resultado moderno de 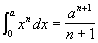 . .
Teoría de Números
El fundador
de la moderna teoría de números, rama de la matemática que estudia
las propiedades de los números, fue el francés Pierre Fermat, quien
no era una matemático profesional, sino un jurista, y su amplia
participación en las matemáticas de su tiempo se realizó casi por
completo a través de correspondencia con otros estudiosos.
Al estudiar
la obra Aritmética de Diofanto, muchos de los aspectos de dicha
obra le fascinaron, incluidos los números perfectos y amigos, las
ternas pitagóricas, los números primos y al divisibilidad. Esta
obra fue comentada por Fermat con numerosas notas al margen y tras
su muerte, su hijo publicó una edición de la aritmética, incluyendo
las anotaciones de su padre. Una de estas notas ha llegado a ser
uno de los más famosos enunciados de toda la historia de las matemáticas,
es decir, fue el célebre y último teorema de Fermat, que dice que
cuando n es mayor que 2, no existe ninguna solución de la ecuación
xn + yn = zn , formada exclusivamente
por números enteros. Este teorema que Fermat afirmaba poder demostrar,
sigue siendo una de los grandes problemas no resueltos, aunque se
han hecho progresos importantes. Ha tenido una gran influencia en
el desarrollo de la teoría de los números, ya que el intento de
demostrarlo ha contribuido a la solución de muchos otros problemas.
Cálculo de Probabilidades
Hay fenómenos
que siempre se repiten de la misma forma, por ejemplo: siempre que
se deja caer una piedra desde lo alto de una torre cae al suelo
con la misma velocidad. Al calentar una barra de metal, el mismo
numero de grados aumenta su longitud en igual cantidad.
Estos tipos
de fenómenos se llaman deterministas.
En todos estos
casos es posible encontrar una ley matemática que relacione las
causas con los efectos producidos.
Pero hay otros
fenómenos que, aún realizándose siempre en las mismas circunstancias,
dan lugar a resultados diferentes; por ejemplo, lanzar una moneda
al aire o echa un dado. En ninguno de estos casos se ha podido encontrar
las causas que determinan el resultado, por lo que se dice que son
debidos al azar.
A tales fenómenos
se les denomina aleatorios, del latín aleaae = suerte, y a cada
uno de los resultados posibles que puede tener cada uno de estos
fenómenos se le denomina suceso.
El cálculo de
probabilidades se inspiro en las preguntas de los jugadores que
buscaban información para ganar en las cartas o en los dados.
Tanto Tartaglia
como Cardano ya habían hecho un sagaz análisis de los problemas
del juego, pero sus obras fueron olvidadas en gran parte.
Alrededor del
año 1651, el caballero De Mère propuso a Pascal algunos problemas
como el siguiente: En una partida de dados intervienen dos jugadores
y apuestan 32 doblones de oro cada uno,, así mismo elige cada uno
un número distinto. Gana el juego el primero que le salga tres veces,
el tiradas alternativas, el número que previamente ha elegido. Después
de un rato de juego, el número elegido por el primer jugador ha
salido 2 veces y el del otro solo una vez. En ese instante, la partida
debe suspenderse. ¿Cómo dividir los 64 doblones de oro apostados?
En la correspondencia
que siguió a este problema, tanto Pascal como Fermat estuvieron
de acuerdo en que el primer jugador tiene derecho a 48 doblones.
Precisamente
de las investigaciones que Pascal y Fermat hicieron sobre las distintas
situaciones del juego d dados, surgirán las bases del cálculo de
probabilidades, que tanto va a influir en aspectos muy diversos
de la vida moderna.
El holandés
Christian Huygens, que publicó en 1657 un breve tratado titulado
Sobre los razonamientos relativos a los juegos de dados, fue quien
primero se inspiro en la correspondencia de Pascal y Fermat. Sin
embargo, el primer tratado importante sobre la teoría de las probabilidades
fue el Arte de la Conjetura, de Jacques Bernoulli: en este trabajo
se reproduce el tratado de Huygens y además contiene el teorema
conocido como teorema de
Bernoulli, que en un lenguaje actualizado dice que 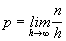 ,
o sea ,
o sea  en la que p es la probabilidad,
n es el numero de veces que se ha presentado el suceso al hacer
h experimentos y e > 0, es decir e es un numero positivo arbitrariamente
pequeño. en la que p es la probabilidad,
n es el numero de veces que se ha presentado el suceso al hacer
h experimentos y e > 0, es decir e es un numero positivo arbitrariamente
pequeño.
La generalización
del teorema de Bernoulli originará la ley de los Grandes Números,
que se puede enunciar: La probabilidad de que la media de una muestra
difiera de la media de la población en una cantidad menor o igual
a e tiende a cero cuando n ® 8 por pequeña que
elijamos e ³ 0. Y se escribe 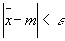 . .
Conviene poner
de manifiesto que de la misma manera que muchos conceptos, a lo
largo de la historia de la matemática, han surgido por la observación
de objetos del mundo físico, también en el cálculo de probabilidades,
el concepto físico o experimental de frecuencia de un suceso dentro
de una experiencia aleatoria le corresponde el concepto teórico
de probabilidad de un suceso.
El análisis combinatorio
Actualmente,
la combinatoria, o el análisis combinatorio, tiene por objeto el
estudio de los distintos agrupamientos y ordenaciones que pueden
recibir los elementos de una conjunto, prescindiendo de la naturaleza
de los mismos. Las cuestiones que se suele considerar son las siguientes:
Las variaciones, las variaciones con repetición, las combinaciones,
las combinaciones con repetición, las permutaciones y las permutaciones
con repetición.
El origen de
esta rama de las matemáticas se remonta a los trabajos de Pascal
y Fermat, pues ambos, al fundamentar el cálculo de probabilidades,
vuelven a encontrar la expresión 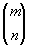 y Pascal es el primero en observar la
relación existente ente restos números y la fórmula del desarrollo
de un binomio. y Pascal es el primero en observar la
relación existente ente restos números y la fórmula del desarrollo
de un binomio.
La expresión
n! que utilizamos hoy para representar el producto de todos los
números naturales desde n hasta 1, ambos incluidos es muy similar
a la expresión m!! que empleo John Wallis para representar el producto
m(m-1)… que termina en 1 o 2 según sea m impar o par.
De la combinatoria
también se ocupo el alemán G. W. Leibniz (1646 - 1716) en su obra
Disertatio de Arte Combinatoria, publicada en 1666. Sin embargo,
el mayor impulsor de esta rama durante el siglo XVII fue Jacques
Bernoulli, quien en su obra, ya mencionada, incluye una teoría general
de permutaciones y de combinaciones que viene facilitada por el
teorema binomial y multinomial.
Precisamente
en esta obra, aparece la primera demostración correcta del teorema
binomial para exponentes enteros y positivos: El desarrollo
del cálculo de probabilidades será decisivo para originar lo que
hoy conocemos como Estadística Matemática.
|
