La base de todos los resultados del Análisis Matemático elemental es el conjunto de los números reales, concebido como un modelo de la continuidad. Por este motivo, para comprender de raíz las propiedades y estructura de dicho conjunto nos parece obligado asumir este concepto. Comenzamos, pues, con la siguiente definición:

Continuo

    Una magnitud o un objeto son continuos si son susceptibles de ser divididos indefinidamente sin perder su carácter.

    Quizás se comprenda mejor qué es la continuidad comparándola con el concepto opuesto: lo discreto.

Discreto

    Una magnitud o un objeto son discretos si cuando se dividen pierden su naturaleza. Es decir, si es imposible dividirlos en magnitudes u objetos del mismo tipo

    La carga eléctrica es una magnitud discreta. En efecto, hasta ahora todas las cargas que se conocen son múltiplos de la carga del electrón (que simbolizaremos mediante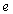). Esta carga elemental no puede dividirse para dar lugar a cargas menores.

    Las conceptos de continuo y discreto son abstractos. En la realidad, no encontramos objetos o magnitudes que sean de uno u otro tipo sino que interpretamos una magnitud o un ente de manera discreta o continua según nuestros propósitos y conocimientos (ver al respecto la observación 1).

    Una descripción matemática de entes y procesos continuos utilizará variables que entre dos valores cualesquiera pueden adoptar un tercer valor. Esto es razonable ya que el proceso o el objeto puede desglosarse indefinidamente en partes que heredan las propiedades del original. Por contra, para describir matemáticamente un objeto o un proceso discreto utilizaremos variables que no pueden adoptar más que unos valores dados y entre dichos valores no hay un tercero.

    La siguiente tabla muestra el número de personas que se encuentran en una parada de autobús hora a hora a lo largo de una mañana.

    El número de personas se considera como una variable discreta ya que no admite valores intermedios entre dos de aquellos que toma (es decir, no es posible encontrar 7,5 personas esperando el autobús). Por otro lado, es razonable admitir que el tiempo debe ser una variable continua ya que entre dos instantes parece hallarse siempre un tercero.

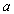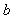    Las magnitudes geométricas: longitud, superficie y volumen, se consideran desde el punto de vista matemático como continuas. De esta forma, una recta se concibe como un agregado de puntos tal que entre dos cualesquiera de ellos y hay siempre un tercero 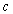(ver figura siguiente).

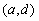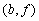    Una superficie se obtiene como el producto cartesiano de una longitud por otra longitud. Es decir, formamos parejas ordenadas de puntos eligiendo el primero de la pareja en una longitud y el segundo en la otra. Esto permite asegurar que entre dos puntos de la superficie y hay siempre un tercero (ver figura siguiente).

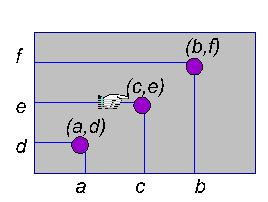
    En el caso del volumen, el producto cartesiano se hace entre tres longitudes y, evidentemente también podremos asegurar la existencia de un tercer punto 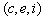entre otros dos 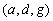y 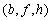(ver figura siguiente).

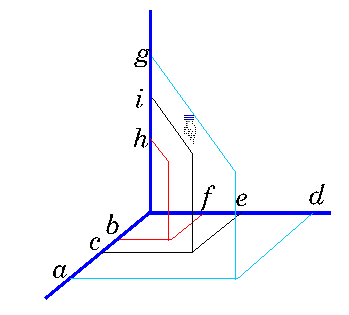
    El lector no debe pensar que las longitudes, superficies y volúmenes reales tienen esta naturaleza. Sabemos que la estructura discreta de la materia junto con el principio de indeterminación de Heisenberg impiden alcanzar un grado de precisión absoluta en la medida de una longitud. Por ello, en una longitud real no es posible asegurar que entre dos puntos haya un tercero.

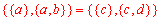
    Un móvil con velocidad constante tarda 3 horas y cuarto en recorrer 200 km. ¿Cuánto tiempo tarda en recorrer 90 km., 120 km. y 180 km.?

    El espacio s recorrido por el móvil se considera una magnitud variable continua pues se trata de una longitud. Como el tiempo recorrido por el móvil se considera una magnitud variable continua pues se trata de una longitud. Como el tiempo t también es una magnitud variable continua, se deduce que la velocidad en un movimiento uniforme: también es una magnitud variable continua, se deduce que la velocidad en un movimiento uniforme:

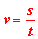
es también una magnitud variable continua.

    En nuestro problema el móvil tarda 3 horas y cuarto en recorrer 200 km., luego su velocidad es:

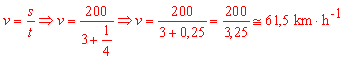
    Una vez sabemos su velocidad el cálculo del tiempo se reduce al cociente

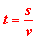
obtenido de la expresión de la velocidad. En particular, el tiempo que tarda en recorre 90 km. es igual a

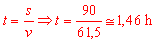
mientras que los tiempos que tarda en recorrer 120 km. y 180 km. son, respectivamente,

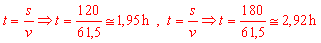
    Los ordenadores procesan información digital, es decir, información fundamentalmente discontinua, como cifras o caracteres alfabéticos, en tanto que los calculadores analógicos tratan información analógica, de carácter esencialmente continuo, como voltajes o intensidades eléctricas.

Los razonamientos matemáticos apoyados en la idea de continuidad son extremadamente potentes y fértiles. Un ejemplo de esto es la deducción de la inconmensurabilidad de la diagonal y el lado del cuadrado.

    Para medir un segmento por medio de otro, vemos cuántas veces cabe uno dentro del otro. Esto es sencillo si el resultado es un número exacto y no queda resto (ver figura siguiente).

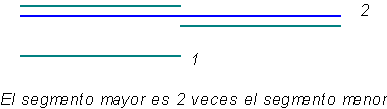
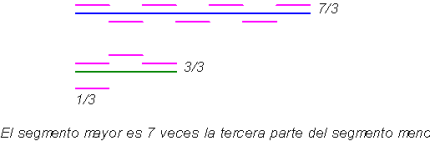
    Si el segmento menor no divide el mayor exactamente, tenemos que fijarnos en el resto. Puede ocurrir que éste sea la mitad, la tercera parte, dos terceras partes, u otra fracción similar del segmento que utilizamos como medida. Si es así, tenemos una especie de medida substitutiva, una fracción del segmento que divide exactamente aquél que estamos midiendo y el que empleamos como medida. El nuevo segmento es una «medida común» para los dos segmentos originales y se dice que estos segmentos son conmensurables (ver figura siguiente).

    Los primeros problemas geométricos indudablemente comprendían una medida común. Por ejemplo, si un rectángulo tiene los lados de 3 y 4 centímetros de longitud, por el teorema de Pitágoras resulta que el cuadrado construido sobre la diagonal tiene por área:

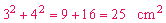
y consecuentemente la diagonal tiene

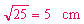
de longitud.

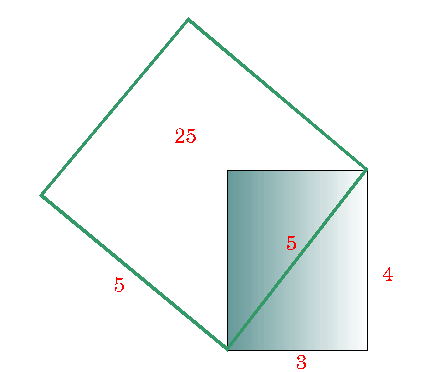
    Puesto que el lado menor del rectángulo y la diagonal tienen un segmento de 1 cm como medida común, están en la proporción 3:5 (ver figura).

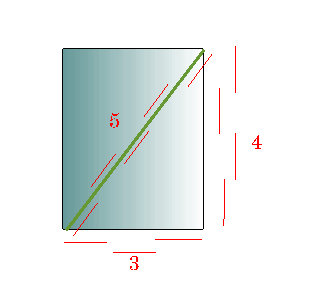
    Es lógico ensayar lo mismo en un cuadrado y buscar otra vez una medida común para el lado y la diagonal. Si intentamos hacerlo, nos encontramos con un resto (ver figura a continuación)

y nos vemos forzados a intentarlo empleando fracciones del lado cada vez menores. La cuestión se plantea en cuanto a la posibilidad de encontrar eventualmente una medida satisfactoria o si simplemente no existe tal medida, es decir, si los dos segmentos son conmensurables o inconmensurables.

    Al suponer que la longitud es una magnitud continua estamos admitiendo que se puede dividir un segmento arbitrariamente en pequeñas secciones y no hay un límite para estas posibles divisiones. En consecuencia, se concluye que el lado y la diagonal de un cuadrado son inconmensurables. Este descubrimiento se atribuye a los Pitagóricos, una sociedad secreta del sur de Italia, acerca del cual poco se sabe con seguridad. Según la leyenda, el pitagórico que hizo públicas estas investigaciones pagó con su vida al perecer en un naufragio. Esto es quizá más alegórico que real, pues es probable que se refiera a los efectos devastadores que tuvo el descubrimiento sobre los fundamentos del pensamiento de la época. En cualquier caso, poseemos el testimonio del propio Platón en sus Leyes, de cómo le entusiasmó este descubrimiento desde el momento en que lo conoció.

    Para demostrar esta inconmensurabilidad debemos empezar por observar ciertos hechos de naturaleza geométrica elemental. Todo el razonamiento es fácilmente reconocible como la

consecuencia de un fallido intento por encontrar una medida común midiendo el lado sobre la diagonal y continuando después el intento de hallar una fracción apropiada. Midamos el lado sobre la diagonal partiendo de B (figura siguiente). Cabe solamente una vez y podemos denominar el punto donde termina como D. A continuación trazamos una línea DB’ perpendicularmente a la diagonal y B’ es el punto donde corta a BC. También unimos A y B’.

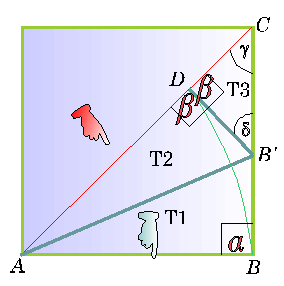
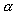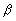    Tenemos entonces el lado AB es igual a AD y el ánguloes igual al ángulo, debido a que ambos son ángulos rectos. Por consiguiente, por uno de los postulados de la igualdad de triángulos, los triángulos T1 y T2 son congruentes y consecuentemente, BB’ y B’D, siendo lados correspondientes en ambos triángulos, son iguales. Por otra parte, el ángulo 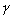formado por un lado del cuadrado y una diagonal, es la mitad de un ángulo recto (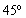) y puesto que el ángulo 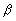fue construido como ángulo recto, sólo queda la mitad de un ángulo recto en el triángulo T3 para el tercer ángulo (ya que la suma de los tres ángulos de todo triángulo tiene que ser igual a 180º). Luego, y T3 es un triángulo isósceles recto y sus lados B’D y CB’ son iguales. Combinando lo que acabamos de demostrar tenemos: BB’ = B’D = DC= r1.

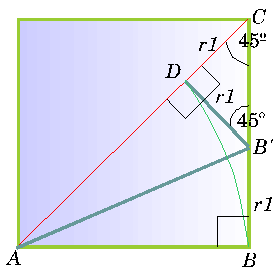
    Esto quiere decir que el resto de la medida de la diagonal con el lado es igual a los lados comunes del triángulo isósceles recto T3.

    Tracemos ahora una perpendicular a la diagonal partiendo de C, de longitud igual a r1 y supongamos que la longitud del lado AB es s.

    Cuando unimos B’ con A’, resulta un cuadrado B’A’CD menor que el inicial. Todo el proceso anterior puede aplicarse ahora al nuevo cuadrado, ya que el resto r1 se mide ahora con la porción de lado B’C.

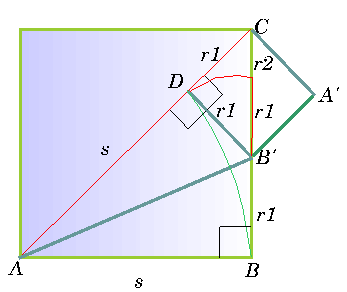
    Como antes obtenemos un resto r2 y podemos escribir:

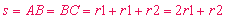
lo que implica que la diagonal AC puede expresarse como:

.

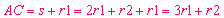    Ahora seguimos el proceso construyendo un nuevo cuadrado que tiene por lado r2 . Al medir este lado r2 utilizando r1 hay un resto r3 .

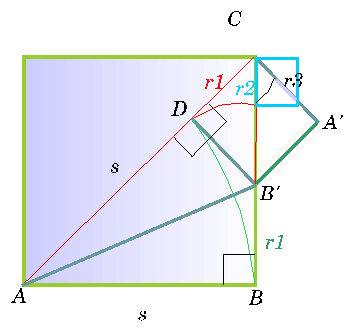
    Este proceso puede seguir indefinidamente gracias a la continuidad de la línea y, en conclusión, no podemos hallar una medida común entre el lado y la diagonal del cuadrado.

  Todo tipo de material, para disfrutar de él completamente On-Line, sin necesidad de descargar archivos ni tener que andar descomprimiendo estos. No te olvides de pasar por el Diccionario, y las secciones Origami y Geointeractiva. Son de lo más interesante.