Un dels primers treballs
sobre el geoplà va ésser del Dr. Caleb Gaetano al 1961. Va ésser
ideat com un recurs didàctic per a l’ensenyament de la geometria
plana elemental.
Jo el vaig conèixer al 1963, en un curs de
didàctica de les matemàtiques, i en sabia també que hi havia adaptacions
per fer geometria de l’espai, és a dir GEOESPAIS. En aquell moment
donava classes a una escola , avui desapareguda, que recollia
alumnes expulsats de totes les de Barcelona pels seus mals resultats.
Un dels grups era de l’últim curs de l’antic “batxillerat elemental”,
(en què seguia una revàlida), de nivell equivalent
al que avui és 2n ESO (sense repetir, 13 a 14 anys) i tenia un
grup de 14 alumnes, tots repetidor o dobles repetidors, totalment
desinteressats pel seu treball, i la part de geometria del programa
era de geometria de l’espai. Vaig pensar que pitjor del que anaven
les coses no podien anar, i vaig fer que el meu pare construís
artesanament un geoplà, adaptat a l’ensenyament de la geometria
del programa del curs, que era geometria de l’espai, per tant
es tracta d’un GEOESPAI: Sobre un taulell de fusta de 50
cm x 50 cm, pintat prèviament de negre, vaig senyalar el centre
d’una circumferència i els vèrtexs d’un hexàgon, i en aquests
punts, seguint les meves instruccions, ell hi va col·locar claus
de ganxo. Després vaig cosir cintes en forma de piràmide, la primera
de base hexagonal.
Amb aquestes “armes” em vaig presentar a classe,
i l’èxit dels resultats em va encoratjar per continuar amb el
seu ús durant anys i presentar-lo avui aquí :
Aquells alumnes n’aprenien i feien bé els exàmens
en qualitat de “lliures”, almenys prou bé per aprovar el curs
i la revàlida. El meu geoespai va quedar dins l’altell d’un armari
amb la llei del 70, que deixava aquest ensenyament a l’EGB, i
ha tornat a ésser actiu amb la reforma
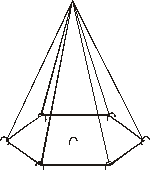
Primer treball : Amb la piràmide hexagonal
Freqüentment he trobat alumnes que, a partir
el dibuix fet a la pissarra, no són capaços d’imaginar la figura
“en relleu”. D’aquesta manera la veuen físicament i després, encara
que els seus propis dibuixos siguin molt dolents (i sovint
ho són), com que la figura “ben feta” és dins el seva memòria,
comprenen l’incomprensible i resolen amb correcció els càlculs,
partint de mides exteriors de la piràmide. El fet de començar
per la piràmide de base hexagonal es deu al fet que, en aquest
cas, la distància “peu de la altura de la piràmide , un vèrtex
de la base” és el radi de la circumferència, i per tant
coincideix amb el costat de l’hexàgon.
Objectiu del treball: Calcular-ne el volum
conegudes les arestes lateral i aresta de la base.
La dificultat és, per a l’alumne, saber “on
hi ha” un triangle rectangle que els permeti usar el teorema de
Pitàgores per calcular l’altura de la piràmide, mesura indispensable
per a poder calcular després el volum.
D’altra part, han d’aprendre a dibuixar ells
la piràmide sobre el seu quadern, condició indispensable perquè
puguin calcular el volum d’una altra piràmide fora de classe.
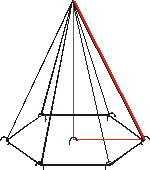
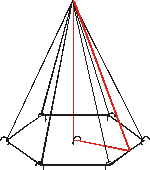
Llavors, en primer lloc, fer la piràmide amb cintes blanques,
i després, amb cintes d’un altre color, fer-los veure els
possibles triangles on podran utilitzar el teorema de Pitàgores.
Segon treball: Amb la piràmide de base quadrada
En primer lloc cal fer una adaptació del geoespai:
Un parell de claus més sobre el taulell de fusta, que, amb dos
dels ja existents, permetran subjectar cintes en forma de quadrat.
Valors coneguts: l’aresta de la base
i l’aresta lateral. Objectiu, calcular el volum, i per tant, cal
trobar l’altura de la piràmide.
a) 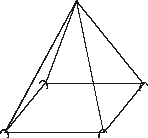
 b)
b) 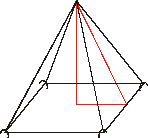 c)
c)
Aparentment més fàcil, no ho és per als alumnes:
En el cas b) han de calcular prèviament la diagonal
del quadrat de la base.
En el cas c) han de calcular prèviament l’apotema
d’una cara.
Tercer treball. El tetraedre regular.
Com que tots els triangles són equilàters,
només tenim una longitud, la del costat. L’objectiu és calcular
el volum
a) 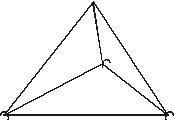
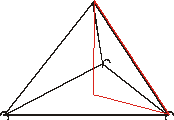 b)
b)
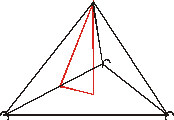 c)
c)
Obliga a revisar les propietats
del triangle equilàter, a fi de calcular
l’altura del triangle de la base, però s’ha de utilitzar després
que també és mediana, i per tant el punt de tall és el baricentre,
que es troba a distància doble del vèrtex
que del costat, propietat aquesta que permet treballar amb el
triangle fet amb cinta vermella, i saber la mesura del catet
que és a la base del geoespai, tant en el cas b) com en el cas
c).
Bibliografia
EL MATERIAL DIDÁCTICO MATEMÁTICO ACTUAL, publicat
por “Publicaciones de la Revista Enseñanza Media", editat
a Madrid, el 1958 en ocasió de la XI Reunió de la Comissió Internacional
para l’estudi y la millora de l’ensenyament matemàtic i
l’exposició internacional simultània, que es varen celebrar a
Madrid del 21 al 27 d’abril de 1957. A aquesta reunió hi varen
assistir Cattegno, E. Castellnuovo, Piaget,
Servais, etc., essent l’ amfitrió
i organitzador Pere Puig Adam. Aquest llibre ve a ésser
el catàleg de l’exposició y en ell s’hi poden veure diversos
models de geoespais.
EL MATERIAL PARA LA ENSEÑANZA DE LAS MATEMÁTICAS,
publicat por l’editorial AGUILAR el 1964. Es una recopilació d’articles
de P. Adam, Cattegno, Castellnuovo, Fletcher, ..., publicada inicialment
en francès por la mateixa CIAEM, també a partir de la mateixa
reunió de Madrid. La versió espanyola és la que va publicar Aguilar.
Alsina, C.; Burgués, C., y Fortuny, J. M. CONSTRUIR
LA GEOMETRÍA. Madrid: Síntesis. Col. Matemáticas: cultura y aprendizaje,
núm. 11, 1988.
Es presenten les dificultats i principis d’un
treball en forma de laboratori. A més d’un conjunt de materials,
es donen instruccions de com fer-los servir, construir-los, etc.
Webgrafia
Hi ha més informació bibliogràfica a
http://www.educa.rcanaria.es/Usr/Apdorta/rematema.htm
Per veure
una bona quantitat d’aparells per fer geometria , entre ells algun
geoespai, es pot anar a la pàgina del
"Museo Universitario di Storia Naturale e della Strumentazione
Scientifica" de la "Università degli studi di Modena
e Reggio Emilia". La direcció és
http://www.museo.unimo.it/theatrum

