|
|
El Paraíso de las Matemáticas - Geointeractiva ~ Prácticas
con Cabri II
 |
|
|
|
.: Geointeractiva
~ Cabri :.
|
|
|
|
|
| Prácticas
con Cabri II |
En esta página se proponen diversos
ejercicios con la intención de que al realizarlos se adquirirá
soltura en el uso del programa. La finalidad de estos ejercicios
no es demostrar, ni aprender propiedades geométricas concretas,
sino familiarizar al que utiliza el programa por primera vez con
el entorno del programa. Los ejercicios no se tienen que realizar
necesariamente en el orden en el que aquí aparecen. Es preferible
elegir los que parezcan más atractivos e intentar realizarlos
en el orden que se desee.
Ejercicio 1: Iniciación
Para empezar, conviene practicar
libremente con las herramientas disponibles en la barra de herramientas.
Para ello puedes empezar utilizándolas y comprobando el funcionamiento
de cada una de ellas descrito en la primera parte del tutorial.
Es conveniente también analizar los
menús que ofrece la "barra de menús" y que, en líneas
generales, se parece al de la mayoría de los programas.
Ejercicio 2: Lugares Geométricos
Lugar geométrico: EJEMPLO 1:
Halla el lugar geométrico descrito por
el incentro de un triángulo ABC inscrito en una circunferencia
cuando uno de sus vétices, por ejemplo C, recorre la circunferencia.
(A y B permanecen fijos).
Dibuja una circunferencia (herramienta
"circunferencia", 4º grupo de herramientas), dibuja
un triángulo cuyos vértices estén sobre la circunferencia (herramienta
"triángulo", tercer grupo de herramientas), etiquete
los vértices como A, B y C ("etiqueta", penúltimo grupo).
Dibuja dos bisectrices señalando el extremo,
origen y extremo de los ángulos, por ejemplo: A, C, B para la
bisectriz del ángulo C y, a continuación: A, B y C para la bisectriz
del ángulo B (herramienta "bisectriz", quinto grupo).
Comprueba que todo funciona bien: mueve
con la herramienta puntero (primer grupo) sucesivamente los tres
vértices y comprueba que la construcción se modifica correctamente
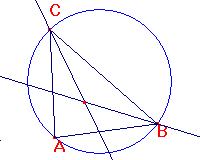
Coloca un punto en la intersección
de las dos bisectrices (herramienta "punto") y etiquétalo
como I.
 Oculta las bisectrices.
Oculta las bisectrices.
 Utiliza ahora la herramienta lugar geométrico (quinto grupo: ),
señala primero el punto que va a dibujar el lugar, es decir el
incentro I, y, a continuación, el punto del que depende el lugar
geométrico, es decir C.
Inmediatamente aparecerá el lugar geométrico
buscado: dos arcos con extremos en A y en B (los extremos no pertenecen
al lugar).
Utiliza ahora la herramienta lugar geométrico (quinto grupo: ),
señala primero el punto que va a dibujar el lugar, es decir el
incentro I, y, a continuación, el punto del que depende el lugar
geométrico, es decir C.
Inmediatamente aparecerá el lugar geométrico
buscado: dos arcos con extremos en A y en B (los extremos no pertenecen
al lugar).
 Utiliza ahora la herramienta "grosor" en el último grupo
y selecciona el lugar geométrico obtenido.
A continuación selecciona la herramienta
"color", también en el último grupo, selecciona el color
verde y marca el lugar geométrico. El resultado obtenido será
parecido al de la siguiente imagen:
Utiliza ahora la herramienta "grosor" en el último grupo
y selecciona el lugar geométrico obtenido.
A continuación selecciona la herramienta
"color", también en el último grupo, selecciona el color
verde y marca el lugar geométrico. El resultado obtenido será
parecido al de la siguiente imagen:
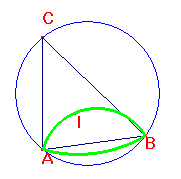
(Ejercicio para el profesor: buscar dónde están los
centros de los arcos de forma experimental con Cabri. Después
tratar de demostrar formalmente el resultado obtenido con Cabri)
Lugar geométrico: EJEMPLO 2:
Halla el lugar geométrico descrito por
el baricentro de un triángulo inscrito en una circunferencia cuando
se mueve uno de sus vértices sobre la circunferencia. Se realiza
de forma parecida al ejercicio anterior.
Lugar geométrico: EJEMPLO 3:
Dibuje una curva podaria siguiendo
las siguientes instrucciones. Se considera una circunferencia
y sobre ella un punto fijo O. Se pide dibujar el lugar geométrico
descrito por las proyecciones de O sobre las rectas tangentes
a la circunferencia. (Se debe situar otro punto P sobre la circunferencia,
dibujar el radio correspondiente a P, obtener la recta tangente
a la circunferencia en P como recta perpendicular al radio que
pasa por P; grupo cuarto. Traza, a continuación la recta que pasa
por O y es perpendicular a la tangente. El punto de corte lo llamaremos
H. Utiliza la herramienta "lugar geométrico" y señala
primero el punto que dibuja el lugar, es decir H, y, después,
el punto del que depende la construcción, P.) Las curvas obtenidas
de esta forma se llaman podarias y en este caso concreto
la podaria obtenida es una cardioide:
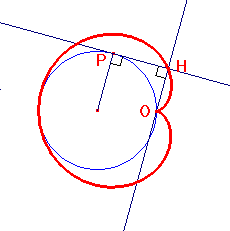
Ejercicio 3: Macros
Se llama macro a la automatización de
un proceso largo que se piensa repetir muchas veces. Por ejemplo,
si deseamos trabajar con propiedades de triángulos en las que
intervenga el baricentro, estaremos obligados a repetir muchas
veces el proceso de obtención del baricentro como intersección
de dos de sus medianas . Se recurre entonces a la creación de
una macro sencilla que permitirá obtener el baricentro de forma
inmediata a partir de un triángulo.
Veamos el proceso en detalle:
Primero abriremos un archivo nuevo, dibujaremos
un triángulo (herramienta "triángulo"), obtendremos
los puntos medios de dos de sus lados (herramienta "punto
medio"), dibujaremos las dos medianas correspondientes (herramienta
"segmento"), obtendremos el punto de intersección (herramienta
"punto") y habremos terminado la construcción del baricentro
de ese triángulo.
Si tenemos previsto repetir a menudo
esta construcción podemos crear una "macro".
Para ello seleccionaremos en el grupo
de herramientas correspondiente (el séptimo, grupo "macros")
"objetos iniciales" pulsaremos sobre el triángulo, seleccionaremos
a continuación "objetos finales" y marcaremos el baricentro.
A continuación deberemos seleccionar "definir macro"
y se abrirá una ventana en la que deberemos asignar obligatoriamente
un nombre a la macro en la casilla "nombre de la construcción",
por ejemplo" construcción baricentro". Si lo deseamos,
podemos asignar un nombre al primer objeto final de la macro.
En este ejemplo sólo hay un objeto final. Llamaremos al objeto
final baricentro; para ello hay que rellenar la casilla correspondiente
escribiendo "baricentro". Luego veremos para qué sirve.
En "ayuda para esta macro"
podemos escribir una pequeña explicación del funcionamiento de
la macro. Esta explicación estará disponible cuando posteriormente
vayamos a utilizar la macro si tenemos activada la ayuda del programa
("barra de menús"). Tendremos así disponible en la parte
inferior de la ventana estas explicaciones que nos permitirán
recordar con qué finalidad fue diseñada y cómo funciona.
El cuadrado junto con la herramienta
de colores permite diseñar un icono, que será asociado a la macro
en el grupo de herramientas. Si no queremos complicarnos la vida
no haremos nada y aparecerá la clásica M.
En el caso de que no activamos
la casilla "guardar como archivo" la macro quedará asociada
al archivo concreto con el que estemos trabajando y cada vez que
abramos ese archivo tendremos disponible la macro. Si queremos
utilizar la macro en cualquier momento, trabajando con cualquier
otro archivo, hay que activar esa casilla. El programa, en ese
caso, nos pregunatará por el nombre del archivo macro (*.mac)
y por el directorio donde deseamos guardarla. Posteriormente cuando
queramos utilizarla en otra sesión de trabajo desde cualquier
otor archivo Cabri sólo necesitaremos decir, con el archivo de
trabajo ya abierto, que queremos incorporar la macro a nuestro
trabajo. Para ello hay que elegir en Archivo/Abrir: "abrir
macro" (*.mac) y la macro estará disponible para ser utilizada
en cuanto lo deseemos.
Cuando la macro está disponible y queramos
utilizarla hay que seleccionarla en el grupo de herramientas "macros",
seleccionar los objetos iniciales, y , automáticamente, se crearán
los objetos finales correspondientes.
El nombre que hayamos asignado al primer
objeto final durante la creación de la macro será visible cuando
pasemos la herramienta "puntero" sobre el primer objeto
creado por la macro.
Ejercicios con Macros:
Crear macros para hallar el baricentro
de un triángulo, su incentro, la circunferencia circunscrita,
inscrita, la de los nueve puntos, para construir triángulos equiláteros
a partir de dos puntos (dos vértices del futuro triángulo) (estudiar
cómo influye el orden en el que se indiquen los dos puntos al
aplicar la macro.
Ejercicio 4: Varios
Observación: Algunos de estos ejercicios están descritos
con detalle más adelante. De momento cada uno puede realizar aquellos
que no planteen dificultad, ya que para algunos requieren explicaciones
adicionales o bien la colaboración de un profesor.
.- Construir un triángulo:
-
Etiquetar los vértices: A, B y C
-
Construir tres rectas a partir de los vértices.
-
Con la herramienta "Grosor" resaltar el triángulo
-
Obtener el incentro y la circunferencia inscrita
-
Ocultar la perpendicular que se ha tenido que dibujar
y, también, el punto de tangencia que se ha utilizado.
-
Construir las tres circunferencias exinscritas
-
Definir una macro llamada "cir_insc_exins" (guardarla
como archivo en el disquete a:\) que permita dibujar a partir
de un triángulo (objeto inicial) sus tres circunferencias
exinscritas, su circunferencia inscrita y el centro de la
circunferencia inscrita (objetos finales).
-
Comprobar su correcto funcionamiento.
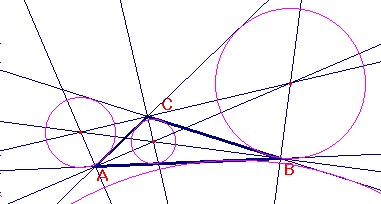
-
Aplicar la macro a un triángulo nuevo, calcular el área
del triángulo (herramienta "área"), medir los
lados. Utilizar la calculadora para comprobar que el área
coincide con el valor obtenido al calcular p*R (p= semiperímetro,
R= radio circ inscr). Añadir con la herramienta "comentario"
las explicaciones necesarias para justificar el resultado.
.- Realizar una construcción similar a la anterior
para obtener el ortocentro de un triángulo y las alturas. Utilizar
la calculadora para hallar el área de tres formas distintas
(utilizando como base cada uno de los tres lados del triángulo).
Justificación de la existencia del ortocentro construyendo un
triángulo cuyos lados pasen por los vértices y cuyos lados sean
paralelos a los lados del triángulo dado. (Es necesario utilizar
alguna propiedad de los paralelogramos; éstas pueden ser motivo
para un estudio particular previo con Cabri)
Modifica la construcción del ortocentro para que
-
Dibujar un triángulo y la paralela media del mismo. Comprobar:
-
que mide la mitad que la base (medir y calcular: dividir
y ver que el resultado es 2,00)
-
que es paralela a la base (herramienta "comprobar
propiedades"-grupo octavo)
-
que los ángulos interiores que forma con los dos lados
con los que es incidente coinciden con los ángulos que forma
la base con ellos. ("ángulo")
.- Dibujar un triángulo y las dos medianas correspondientes
a los vértices de la base ( A y B). Dibujar el punto de corte
de ambas medianas (AM y AN) y etiquetarlo como G. Dibujar la
paralela media NM del triángulo ABC y, también, la paralela
media del triángulo ABG (PQ) . Dibujar el cuadrilátero PQMN
y convencerse de que es un paralelogramo. Utilizando la propiedad
característica de las diagonales de un paralelogramo, encontrar
la relación métrica entre AG y GM y, también, entre BG y GN.
Justificar que la tercera mediana también tiene que pasar necesariamente
por G.
.- Recta de Euler: En todo triángulo ABC el baricentro,
el ortocentro y el circuncentro están alineados y existe una
relación métrica interesante. Investigar el asunto.
.- Triángulos de Napoleón: construir triángulos equiláteros
sobre los lados de un triángulo cualquiera y hacia fuera. Comprobar
que sus baricentros determinan un triángulo equilátero llamado
triángulo de Napoleón exterior. Construir el triángulo de Napoleón
interior y comprobar que es equilátero. Comprobar que la diferencia
de las áreas de los dos triángulos de Napoleón coincide con
el área del triángulo. (La construcción de los triángulos y
de su baricentro se puede realizar definiendo una macro de forma
que a partir de dos puntos (objetos iniciales) construya un
triángulo equilátero y su baricentro (objetos finales); al aplicar
la macro, del orden en el que se indiquen los puntos, dependerá
que el triángulo resultante se construya hacia un lado u otro
del segmento determinado por los dos puntos)
.- Triángulo de Morley: Trisecar los ángulos del triángulo
ABC y comprobar los puntos de corte correspondientes determinan
un triángulo equilátero llamado triángulo de Morley (demostración
en Coxeter: Introducción a la Geometría)
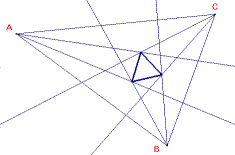
.- Dibujar un triángulo rectángulo y construir sobre
los catetos y sobre la hipotenusa cuadrados, medir las áreas
y, utilizando la calculadora, realizar una comprobación empírica
del teorema de Pitágoras. Idem construyendo triángulos equiláteros,
hexágonos o cualquier tipo de polígonos construidos sobre los
lados con la condición de que sean semejantes. (Utilizar macros
para la construcción de los polígonos regulares sobre los lados).
.- Dibujar una circunferencia, una cuerda y comprobar
que los ángulos inscritos que abarcan dicha cuerda (es decir:
el mismo arco) coinciden. Comprobar la relación con el ángulo
central correspondiente y diseñar una tabla que recoja los datos
de cinco posiciones distintas.
Algunas Ideas para Experimentar
Las ideas que presentamos a continuación pretenden
servir de ayuda a profesores para diseñar actividades
de entrenamiento-aprendizaje con Cabri:
.- Arco capaz.
.- Comprobar empíricamente la propiedad de la potencia de un punto
exterior respecto de una circunferencia. Realizando la construcción
oportuna y viendo que existen dos triángulos semejantes deducir
el resultado a partir de la proporcionalidad correspondiente.
.- Teorema de la bisectriz.
.- Circunferencia trigonométrica.
.- Elipse sencilla (macro).
.- Elipse macro a partir de focos y un punto.
.- Ley de Snell: tangentes a una elipse.
.- Semejanza de triángulos, razón de semejanza y de las áreas.
.- Hipérbolas y parábolas. Macros. Tangencias.
.- Haces de rectas, pendientes, paralelismo, perpendicularidad
y ecuaciones.
.- Ejercicios de optimización: punto de Fermat y triángulo órtico.
.- Otras propiedades del triángulo órtico.
.- Ejercicios de gráficas de funciones sencillas.
.- Ejercicios de gráficas de funciones asociadas a problemas geométricos.
|
|
|
|
|
|
|
